مقدار موثر یا RMS

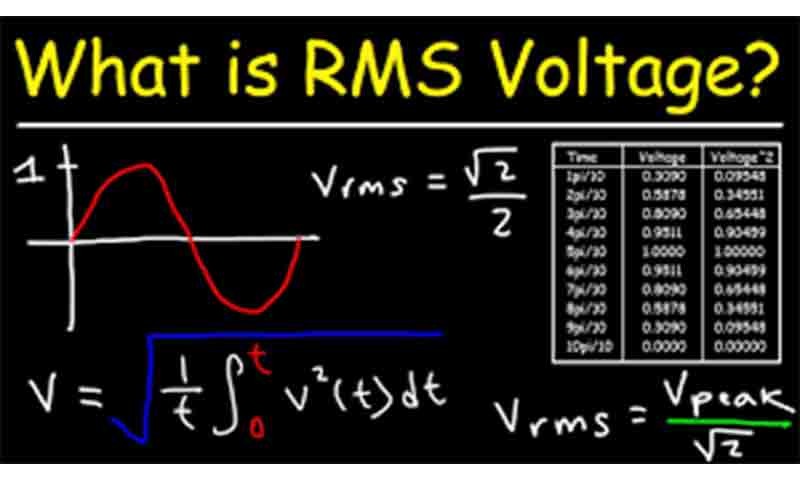
ریشه میانگین مربع, جذر مجذور میانگین ,ریشه مقدار متوسط توان دوم یا ریشه میانگین مربع، که معمولا RMS نامیده می شود، یک مفهوم مهم در الکترونیک است. همچنین یکی از مواردی است که می تواند در ابتدا کمی سردرگمی ایجاد کند. در این مقاله کوتاه به تعریف RMS، چرایی نیاز و نحوه استفاده از آن می پردازیم. ما همچنین تفاوت بین RMS "متوسط" یا AVARGE RMS و RMS "واقعی" یا TRUE RMS را توضیح می دهیم.

تعریف RMS
RMS یک مفهوم ریاضی است که برای استخراج میانگین یک مقدار دائما متغیر استفاده می شود. در الکترونیک، RMS راهی برای محاسبه توان AC موثر ارائه می دهد. به بیان دیگر، RMS مقدار گرمایش برق AC را به گونه ای تعیین می کند که به ما امکان می دهد آن را با مقدار گرمایش معادل یک سیستم DC مقایسه کنیم.

برای کمک به درک این موضوع، اجازه دهید منبع تغذیه DC مانند باتری 9 ولت را در نظر بگیریم. اگر ولتاژ این باتری (بدون بار) را روی نموداری با زمان به عنوان محور افقی رسم کنیم، در نهایت به یک خط مستقیم می رسیم. نمودار از 9 ولت شروع می شود و برای عمر قابل استفاده باتری کم و بیش ثابت می ماند. در این مورد، اندازه گیری ولتاژ ساده است: ما به سادگی هر نقطه ای را در نمودار انتخاب می کنیم، و این مقدار را به ما می دهد.

توجه داشته باشید که نمودار خط مستقیم ما تا حدودی ایده آل است. در یک سیستم با بار واقعی، ولتاژ به تدریج در طول زمان به سمت پایین شیب خواهد داشت. اما نقطه مرکزی ما ثابت می ماند: تنها کاری که برای تعیین ولتاژ باید انجام دهیم این است که هر لحظه به سادگی اندازه گیری کنیم.
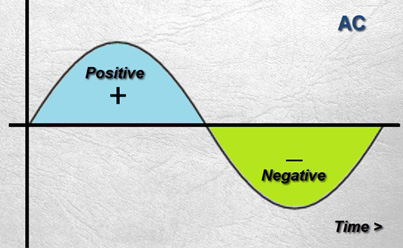
برای برق AC، اوضاع بسیار پیچیده تر است. هنگامی که توان AC تمیز و بدون اعوجاج را در برابر زمان رسم می کنیم، نمودار موج سینوسی آشنا را می بینیم، به دلیل چرخه ثابت آن از مقادیر مثبت به منفی و سپس دوباره.

اگر ولتاژ یا جریان را در زمان های تصادفی در این نمودار اندازه گیری کنیم، بسته به اینکه کدام نقطه را انتخاب می کنیم، مقادیر متفاوتی به دست می آوریم. در نگاه اول، ممکن است منطقی به نظر برسد که صرفاً میانگین این اندازه‌گیری‌ها را برای محاسبه توان مؤثر برای این منبع محاسبه کنیم. با این حال، اگر این کار را انجام دهیم، در نهایت با ولتاژ یا جریان صفر مواجه خواهیم شد. طبق تعریف، چرخه موج AC سینوسی خالص به همان مقدار که بالای نمودار است، به همان مقدار نیز زمان زیر نمودار ( زیر صفر ) را می گذراند، بنابراین مقادیر منفی مقادیر مثبت را خنثی می کند.

بنابراین مهم نیست که اوج توان ما چقدر بالا باشد، میانگین توان برای سیستم AC کلاسیک همیشه صفر خواهد بود، همان طور که اصلاً منبع تغذیه نداریم. بدیهی است که چنین نتیجه ای چیزی در مورد جریان برق واقعی در این سیستم به ما نمی گوید، بنابراین ما به روش دیگری برای استخراج ولتاژ یا جریان متناوب موثر نیاز داریم.

محاسبه RMS
ما می توانیم این کار را با استفاده از روش RMS انجام دهیم. برای اهداف نمایشی و فرضی، ساده‌ترین و «پاک‌ترین» شکل موج AC را در نظر می‌گیریم، یک موج سینوسی بدون اعوجاج مانند آنچه در بالا نشان داده شده است. در زندگی واقعی یک سیستم AC دارای عدم تقارن شکل موج است به دلیل عواملی مانند بارهای غیرخطی. کمی بعد در این مقاله به این نکته باز خواهیم گشت. اما در حال حاضر، بیایید در مورد چگونگی پیدا کردن RMS برای یک موج سینوسی معمولی بحث کنیم.
اولین قدم مربع مقادیر توان AC است. با این کار نموداری شبیه به نمودار زیر ایجاد می شود.

همانطور که می بینید، تمام نقاط نمودار روی صفر یا بالاتر از آن هستند، بنابراین دیگر مجبور نیستیم با مقادیر منفی سر و کار داشته باشیم. اکنون می توانیم از این اعداد مثبت برای محاسبه توان موثر این سیستم AC استفاده کنیم. استخراج گام به گام این محاسبات به مقدار متوسطی از دانش ریاضی نیاز دارد.
بنابراین به منظور اختصار ما را دنبال کنید تا فرمول نهایی را نشان دهیم که برای ولتاژ سینوسی به صورت زیر است:

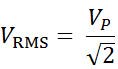
در این معادله، ولتاژ RMS (VRMS) برابر است با اوج ولتاژ AC (VP) تقسیم بر 2√. برای مثال، فرض کنید یک سیستم AC داریم که در آن پیک ولتاژ 170 ولت است. با استفاده از فرمول نشان داده شده در بالا، یک مقدار VRMS تقریباً 120 ولت بدست می آوریم. به عبارت دیگر، ولتاژ موثر این سیستم AC برابر با ولتاژ خروجی خانگی در ایالات متحده آمریکا 120 ولت است.

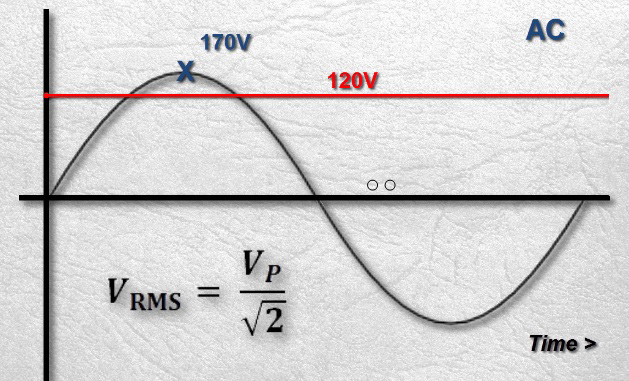
این فرمول همچنین می تواند برای محاسبه جریان AC موثر اعمال شود:

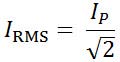
و برای یک تقریب سریع، می توانید ولتاژ یا جریان موثر را با ضرب مقدار پیک در 0.707 محاسبه کنید، که شکل اعشاری 1/√2 را نشان می دهد:

Vrms= Vp x 0.707

RMS واقعی
این معادله ساده، اساس ابزارهای به اصطلاح "میانگین" RMS یا AVRAGE RMS را تشکیل می دهد. برای سیستم های الکتریکی که چرخه AC سینوسی است و به طور منطقی اعوجاج ندارند و تولید هارمونیک نمیکنند، این محصولات می توانند نتایج دقیق و قابل اعتمادی را تست و ارائه دهند. متأسفانه، برای سایر شکل‌های موج AC، مانند موج‌های مربعی، این محاسبه می‌تواند عدم دقت قابل توجهی را ایجاد کند.
هنگامی که موج AC نامنظم است، این معادله می تواند مشکل ساز باشد، همانطور که در واقعیت سیستم هایی وجود دارند که شکل موج اصلی توسط یک یا چند موج هارمونیک دچار اعوجاج شده است.

در این موارد، ما باید از روشی به نام "RMS واقعی" یا TRUE RMS استفاده کنیم که شامل یک سری محاسبات ریاضی تعمیم‌یافته‌تر است که تمام بی‌نظمی‌ها و عدم تقارن‌هایی را که ممکن است در شکل موج AC وجود داشته باشد، در نظر می‌گیرد:

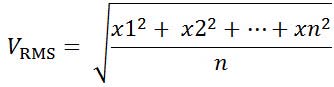
... که در آن n برابر است با تعداد اندازه گیری های انجام شده در طول یک چرخه کامل شکل موج که برای تجهیزات Chauvin Anoux، همیشه مضربی از 2 است (معمولاً 64، 128 یا 256 بسته به تجهیز). هرچه این عدد بیشتر باشد، محاسبه RMS دقیق تر خواهد بود. دلیل آن این است که هر چه مقدار n بیشتر باشد، بر اساس فرمول داده شده در بالا می توان ترتیب هارمونیک های بالاتری را در  آن جای داد.
برای درک اینکه چرا چنین است، بیایید مثال زیر را در نظر بگیریم. فرض کنید یک موج هارمونیک سوم را به شکل زیر به موج اصلی خود اضافه کرده ایم:

ترکیب این دو موج شکل موج ناهموار زیر را ایجاد می کند:

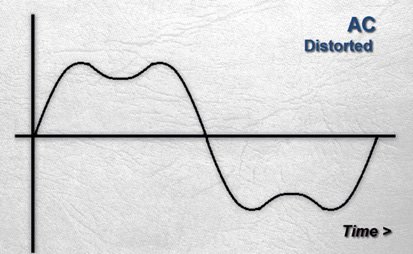
همانطور که می بینید، بیشترین اعوجاج در اصل زمانی رخ می دهد که هارمونیک سوم به اوج مثبت یا منفی خود برسد. طبق تعریف، این اتفاق 6 بار در هر چرخه طبیعی کامل اتفاق می افتد.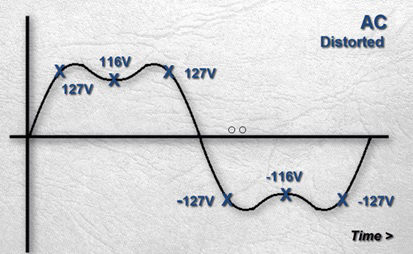
بنابراین برای انطباق با اثر هارمونیک سوم، ما 6 اندازه گیری را انجام می دهیم که با قله های مثبت و منفی هارمونیک سوم مطابقت دارد:

از آنجایی که در این مثال ما 6 اندازه گیری داریم، مقدار n برابر با 6 است. با وارد کردن این عدد و مقادیر اندازه گیری به فرمول، موارد زیر را به دست می آوریم:

... یا تقریباً 123 ولت:

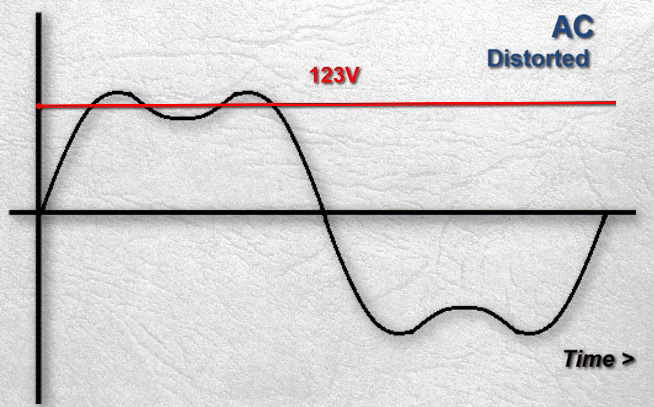
به عبارت دیگر، اعوجاج هارمونیک معرفی شده در شکل موج نشان داده شده در بالا، VRMS را از 120 ولت در شکل سینوسی خالص به تقریباً 123 ولت در شکل دارای هارمونیک آن تغییر داده است.
توجه داشته باشید که این یک مثال بسیار ساده است. در دنیای واقعی، احتمالاً نیاز داریم که بسیاری از رتبه های هارمونیکی دیگر را نیز در نظر بگیریم، (5، 7، 9، 11 و غیره)، که در این صورت تعداد اندازه‌گیری‌ها در هر چرخه، و به ترتیب مقدار n، بسیار بالاتر خواهد بود. اما برای ما به عنوان یک هدف نمایشی، مثال داده شده باید بینشی در مورد چگونگی انجام محاسبات تجهیزات دارای RMS واقعی یا True Rms به شما ارائه کرده باشد.
امیدواریم این توضیح مختصر در مورد میانگین مربعات ریشه برای شما مفید بوده باشد. اگر سؤالات بیشتری در مورد این موضوع دارید یا پیشنهاداتی برای مقالات بعدی دارید، لطفاً به ما ایمیل بزنید:

www.yektamut.com

Info@yektamut.com